Solución Problema 2 de Ecuación de Continuidad

De forma similar al ejemplo anterior, en este problema de Ecuación de Continuidad , debemos reforzar el concepto principal que es la utilización correcta de la fórmula, con este ejercicio lo terminará de comprender, no olvide que con estos ejercicios se proporciona la solución paso a paso del ejemplo y nuevamente el alumno comprueba sus resultados de manera correcta y concisa. 😊👇

Nivel de Dificultad: ⭐⭐

Problema 4.- Un túnel de agua tiene una sección transversal circular que se restringe de un diámetro de 3.6 metros a la sección de prueba, que es de 1.2 metros de diámetro. Si la velocidad de flujo es de 3 m/s en el tubo de diámetro mayor, determine la velocidad del fluido en la sección de prueba.

Ecuación de Continuidad Problema 1

Solución:

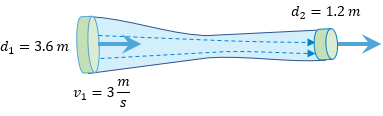
Al igual que el problema 3, el problema 4 es muy similar para su solución. El problema describe un túnel con un diámetro de 3.6 metros y que después se reduce en una sección de prueba de 1.2 metros, a su paso el flujo de agua es de 3 m/s pero, ¿qué ocurre cuando este flujo atraviesa la sección reducida?, esto es lo que vamos a calcular empleando nuevamente la ecuación de continuidad 😀

Obtener la velocidad del fluido en la sección de prueba

Datos:

$\displaystyle {{d}_{1}}=3.6m$

$\displaystyle {{d}_{2}}=1.2m$

$\displaystyle {{v}_{1}}=3\frac{m}{s}$

a) Obtener la velocidad del fluido en la sección de prueba

Recordemos que la ecuación de continuidad, está expresada de la siguiente forma:

$\displaystyle {{A}_{1}}{{v}_{1}}={{A}_{2}}{{v}_{2}}$

El problema nos pide encontrar la velocidad final, es decir a "V2" , entonces despejamos:

$\displaystyle {{v}_{2}}=\frac{{{A}_{1}}{{v}_{1}}}{{{A}_{2}}}$

Antes de sustituir nuestros datos, debemos de encontrar primero las áreas

♦ Encontrando el área de las secciones

⭕ Área 1

$\displaystyle {{A}_{1}}=\frac{\pi {{d}_{1}}^{2}}{4}=\frac{\pi {{\left( 3.6m \right)}^{2}}}{4}=10.178{{m}^{2}}$

⭕ Área 2

$\displaystyle {{A}_{2}}=\frac{\pi {{d}_{2}}^{2}}{4}=\frac{\pi {{\left( 1.2m \right)}^{2}}}{4}=1.131{{m}^{2}}$

Ahora si podemos sustituir en la fórmula, para encontrar la velocidad final:

$\displaystyle {{v}_{2}}=\frac{{{A}_{1}}{{v}_{1}}}{{{A}_{2}}}=\frac{\left( 10.178{{m}^{2}} \right)\left( 3\frac{m}{s} \right)}{1.131{{m}^{2}}}=27\frac{m}{s}$

Por lo que la velocidad de la sección reducida en el tunel es de 27 m/s

Resultado:

$\displaystyle {{v}_{2}}=27\frac{m}{s}$

Deja una respuesta Cancelar la respuesta