Solución Problema 2 de La Ley de los Gases Ideales

De forma similar al ejemplo anterior, en este problema de La ley de los gases ideales , debemos reforzar el concepto principal que es la utilización correcta de la fórmula, no olvide que con estos ejercicios se proporciona la solución paso a paso del ejemplo y nuevamente el alumno comprueba sus resultados de manera correcta y concisa. 😊👇

Nivel de Dificultad: ⭐⭐

Problema 4.- Una masa de oxígeno gaseoso ocupa un volumen de 70 litros en un recipiente que se encuentra a una presión de 1.5 atmósferas y a una temperatura de 298K. Determinar: a) cuántos moles de oxígeno tiene.

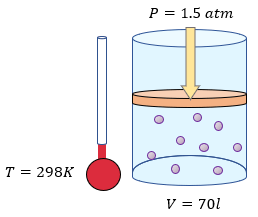
problema de los gases ideales o gases perfectos

Solución:

Este problema es muy similar al ejemplo 1, y lo que nos pide el problema es encontrar la cantidad de número de moles que hay en la masa de oxígeno en las condiciones que nos comenta, tales como la del volumen de 70 litros, la presión de 1.5 atmósferas y una temperatura en grados kelvin de 298. Ahora lo que tenemos que realizar es anotar nuestros datos:

Obtener el número de moles de oxígeno

Datos:

$\displaystyle V=70l$

$\displaystyle P=1.5atm$

$\displaystyle T=298K$

$\displaystyle R=0.0821\frac{atm\cdot l}{mol\cdot K}$

a) Obtener el número de moles de oxígeno

Para poder obtener el número de moles, debemos analizar nuestra ecuación de gas ideal.

$\displaystyle PV=nRT$

Despejamos a "n" de la fórmula y obtenemos:

$\displaystyle n=\frac{PV}{RT}$

Ahora simplemente sustituimos nuestros datos en la fórmula:

$\displaystyle n=\frac{PV}{RT}=\frac{\left( 1.5atm \right)\left( 70l \right)}{\left( 0.0821\frac{atm\cdot l}{mol\cdot K} \right)\left( 298K \right)}=\frac{105atm\cdot l}{24.47\frac{atm\cdot l}{mol}}=4.3mol$

Esto nos da el resultado de 4.3 moles

Resultado:

$\displaystyle n=4.3mol$

Deja una respuesta Cancelar la respuesta