Solución Problema 2 de la Ley General del Estado Gaseoso

De forma similar al ejemplo anterior, en este problema de La ley general del estado gaseoso , debemos reforzar el concepto principal que es la utilización correcta de la fórmula, no olvide que con estos ejercicios se proporciona la solución paso a paso del ejemplo y nuevamente el alumno comprueba sus resultados de manera correcta y concisa. 😊👇

Nivel de Dificultad: ⭐⭐

Problema 4.- Una masa de hidrógeno gaseoso ocupa un volumen de 0.7 litros a una temperatura de 28 °C y a una presión absoluta de 850 mm de Hg. ¿Cuál será su presión absoluta si su temperatura aumenta a 98°C y su volumen es de 1.6 litros?

Ley general del estado gaseoso

Solución:

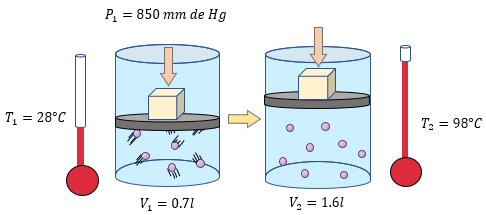
A diferencia del problema 3, en este problema si nos indican cuales son las condiciones iniciales y finales de la temperatura y volumen, así como la presión inicial. Por lo que sabemos que lo que debemos calcular es la presión final, pero como hemos dicho, afortunadamente tenemos varios datos que nos servirán para la solución del problema de manera directa 😀

Obtener la presión absoluta final

Datos:

$\displaystyle {{P}_{1}}=850mmdeHg$

$\displaystyle {{V}_{1}}=0.7l$

$\displaystyle {{T}_{1}}=28{}^\circ C+273=301K$

$\displaystyle {{V}_{2}}=1.6l$

$\displaystyle {{T}_{2}}=98{}^\circ C+273=371K$

Ahora si podemos empezar a resolver el ejercicio.

a) Obtener la presión absoluta final

Recordemos que la fórmula de la ley general del estado gaseoso es:

$\displaystyle \frac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\frac{{{P}_{2}}{{V}_{2}}}{{{T}_{2}}}$

El problema nos pide calcular la presión final, o sea P2, entonces lo despejamos:

$\displaystyle {{P}_{2}}=\frac{{{P}_{1}}{{V}_{1}}{{T}_{2}}}{{{V}_{2}}{{T}_{1}}}$

Ahora es momento de sustituir nuestros datos en la fórmula:

$\displaystyle {{P}_{2}}=\frac{{{P}_{1}}{{V}_{1}}{{T}_{2}}}{{{V}_{2}}{{T}_{1}}}=\frac{\left( 850mmdeHg \right)\left( 0.7l \right)\left( 371K \right)}{\left( 1.6l \right)\left( 301K \right)}=458.35mmdeHg$

Por lo que la presión final es de 458.35 mm de Hg

Resultado:

$\displaystyle {{P}_{2}}=458.35mmdeHg$

Deja una respuesta Cancelar la respuesta