Solución Problema 4 de Campo Eléctrico

Este problema es quizá uno de los problemas más interesante que los anteriores, precisamente porque involucran más datos que debemos conocer hasta ahora en el tema de Campo Eléctrico, tal como temas de suma de vectores de forma analítica, así también como los despejes de fórmulas y conversión de unidades. Si dominamos estos temas, no tendremos mucha complicación a la hora de solucionar problemas de éste tipo, por eso hemos calificado a este ejercicio con un nivel de dificultad de 4/5. Esperando que el alumno refuerce por completo este tópico de Física y pueda dominar muy bien el electromagnetismo. 😊👇

Nivel de Dificultad: ⭐⭐⭐⭐

Problema 8.- Determinar la magnitud resultante de la intensidad del campo eléctrico en el punto P dirigido por dos cargas puntuales q1 = 7μC y q2 = -2μC Distribuidas de la siguiente manera: Observar la imagen.

Problema de Campo Eléctrico

Solución:

Si no tenemos conocimiento sobre la suma de vectores y su descomposición rectangular entonces tendremos problemas, pero aquí en nuestro sitio web podrás encontrar varios ejercicios de vectores que te servirán para aprender mucho mejor este tema y no tener problemas con la solución de este ejercicio. En principio no es complicado este ejemplo pero si requiere mucho más cálculo que los ejercicios anteriores, por eso lo hemos dejado al final.

Obtener la magnitud de la intensidad del campo eléctrico

Datos:

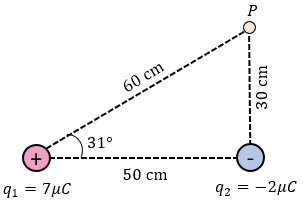
$\displaystyle {{q}_{1}}=7x{{10}^{-6}}C$

$\displaystyle {{q}_{2}}=-2x{{10}^{-6}}C$

$\displaystyle {{d}_{1}}=60cm\left( \frac{1m}{100cm} \right)=0.6m$

$\displaystyle {{d}_{2}}=30cm\left( \frac{1m}{100cm} \right)=0.3m$

a) Obtener la magnitud resultante de la intensidad del campo eléctrico

Lo primero que haremos será calcular la magnitud de la intensidad del campo eléctrico ocasionado por la carga q2, al ser ésta una carga negativa el campo eléctrico irá verticalmente hacia abajo, por lo que será negativo. De esta forma:

♦ Calculando $\displaystyle {{E}_{2}}$

$\displaystyle {{E}_{2}}=-\frac{K{{q}_{2}}}{{{d}_{2}}^{2}}$

Sustituyendo nuestros datos en la fórmula, obtenemos:

$\displaystyle {{E}_{2}}=-\frac{K{{q}_{2}}}{{{d}_{2}}^{2}}=-\frac{\left( 9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}} \right)\left( 2x{{10}^{-6}}C \right)}{{{(0.3m)}^{2}}}=-2x{{10}^{5}}\frac{N}{C}$

Es decir:

$\displaystyle {{E}_{2}}=-2x{{10}^{5}}\frac{N}{C}$

♦ Calculando $\displaystyle {{E}_{1}}$

Nuestra fórmula para la intensidad del campo en la carga 1 será de:

$\displaystyle {{E}_{1}}=\frac{K{{q}_{1}}}{{{d}_{1}}^{2}}$

Sustituyendo nuestros datos en la fórmula, obtenemos:

$\displaystyle {{E}_{1}}=\frac{K{{q}_{1}}}{{{d}_{1}}^{2}}=-\frac{\left( 9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}} \right)\left( 7x{{10}^{-6}}C \right)}{{{(0.6m)}^{2}}}=1.75x{{10}^{5}}\frac{N}{C}$

El vector de la intensidad del campo E1 puede ser descompuesta en sus dos componentes vectoriales, (Tanto en "x", como en "y"), entonces hacemos el siguiente cálculo:

$\displaystyle {{E}_{1x}}={{E}_{1}}\cos 31{}^\circ =\left( 1.75x{{10}^{5}}\frac{N}{C} \right)\cos 31{}^\circ =1.5x{{10}^{5}}\frac{N}{C}$

Ahora hacemos lo mismo para "y"

$\displaystyle {{E}_{1y}}={{E}_{1}}sen31{}^\circ =\left( 1.75x{{10}^{5}}\frac{N}{C} \right)sen31{}^\circ =0.90x{{10}^{5}}\frac{N}{C}$

♦ Obteniendo la resultante de todas las componentes tanto en "x" como en "y" del Campo eléctrico

$\displaystyle {{E}_{Rx}}=\sum{{{E}_{x}}=}{{E}_{1x}}=1.5x{{10}^{5}}\frac{N}{C}$

$\displaystyle {{E}_{Ry}}=\sum{{{E}_{y}}=}{{E}_{1y}}+\left( -{{E}_{2y}} \right)=0.90x{{10}^{5}}\frac{N}{C}-2x{{10}^{5}}\frac{N}{C}=-1.1x{{10}^{5}}\frac{N}{C}$

♦ Obteniendo la magnitud de la resultante:

$\displaystyle {{E}_{R}}=\sqrt{{{\left( {{E}_{Rx}} \right)}^{2}}+{{\left( {{E}_{Ry}} \right)}^{2}}}=\sqrt{{{\left( 1.5x{{10}^{5}}\frac{N}{C} \right)}^{2}}+{{\left( -1.1x{{10}^{5}}\frac{N}{C} \right)}^{2}}}$