Solución Problema 4 de la Ley de Charles

Con este cuarto problema de la ley de Charles el alumno termina aplicando y utilizando no solo las condiciones finales, sino también las condiciones iniciales para así poder encontrar las incógnitas ya sea de temperatura o volumen inicial, y así el alumno pueda comprobar nuevamente la utilidad de ésta ley. Recuerde que muchas veces es importante revisar nuestra gráfica de proporcionalidad entre volumen vs temperatura, para tener una idea del resultado que podríamos obtener. 😊👇

Nivel de Dificultad: ⭐⭐

Problema 6.- Calcular la temperatura absoluta a la cual se encuentra un gas que ocupa un volumen de 0.4 litros a una presión de una atmósfera, si a una temperatura de 45°C ocupa un volumen de 1.2 litros a la misma presión.

problema de la ley de charles

Solución:

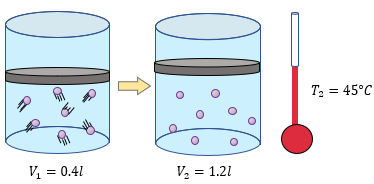
Al leer el enunciado del problema nos percatamos de inicio, que las condiciones iniciales no las proporcionan, sino que ahora es al revés, nos piden la temperatura absoluta inicial del gas cuando tenía 0.4 litros de volumen, después a 45°C el volumen aumentó a 1.2 litros, recordemos que la gráfica de la ley de charles es proporcional, es decir que a mayor temperatura mayor volumen, a menor temperatura, menor volumen. Entonces lo que buscamos realmente es una temperatura que tiene que ser menor a la temperatura final.