Principio de Bernoulli – Ejercicios Resueltos

En Fisimat hemos pensado mucho para crear el título de éste artículo, ya que existen diversas variantes de nombre dependiendo el autor o investigador. Podemos encontrar éste tema con el nombre del Principio de Bernoulli también cómo el Teorema de Bernoulli y en otras fuentes de varios autores que han realizado libros importantes de Física , lo han nombrado también como la Ecuación de Bernoulli , pero aclaramos ante todos, que estos nombres relacionan exactamente a lo mismo. No se confundan si en algún momento mencionamos un nombre y luego otro. Esto es con la finalidad de familiarizarse con las definiciones y que no nos tomen en curva nuestros conocimientos 😎

Bien ahora es momento de comenzar y vamos a partir de la teoría que necesitamos conocer, porque sin esa teoría no comprenderemos en absoluto la solución de los ejercicios o ejemplos aquí propuestos para su desarrollo. Hasta ahora hemos hablado de los parámetros de presión, densidad, y velocidad. Pero hace falta mencionar a la altura que simbolizaremos con una letra “h”, en algunos libros de mecánica de fluidos lo hacen con una “z”, bien a la altura se le toma dependiendo de algún nivel de referencia. Pues bien, el primero en relacionar éstas cantidades fue el gran matemático suizo Daniel Bernoulli (1700 – 1782).

🤔 ¿Quién fue Daniel Bernoulli?

Aquí una pequeña Biografía de el Daniel Bernoulli.

Daniel Bernoulli nació en Suiza y realizó grandes contribuciones en la dinámica de fluidos, publicó su obra más famosa en 1738 titulada “Hidrodinámica“, donde advertía sobre el estudio teórico y práctico del equilibrio, la presión y la rapidez en los fluidos. De allí deduce el “Principio de Bernoulli” un concepto que expresa que a medida que aumenta la rapidez de un fluido , su presión disminuye. Con esto la ley de la conservación de la energía se cumple cuando los líquidos están en movimiento, de allí deduce el siguiente enunciado:

En un líquido ideal cuyo flujo es estacionario, la suma de aquellas energías como la cinética, potencial y de presión (o energía de flujo) que posee cierto líquido en un punto, es igual a la suma de éstas energías en otro punto cualquiera.

Esto daba un cambio rotundo al conocimiento que se tenía de los fluidos en ese tiempo, ya que a pesar que se dedujo solo para fluidos, en los gases es aplicable también.

🔸 Deducción de la ecuación de Bernoulli

Para deducir la ecuación de lo que proponía Bernoulli en su libro, es necesario considerar la siguiente imagen.

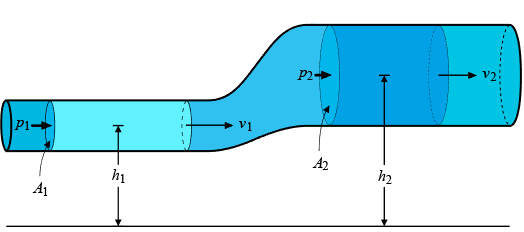
Como se basa en la ley de la conservación de la energía, entonces deducimos los siguientes tres tipos:

1.- Energía cinética: Debido a la velocidad y a la masa del líquido. Denotada por la siguiente fórmula:

$\displaystyle {{E}_{c}}=\frac{1}{2}m{{v}^{2}}$

2.- Energía potencial: Debido a la altura del líquido, respecto a cualquier punto de referencia, y dada por la siguiente fórmula:

$\displaystyle {{E}_{p}}=mgh$

3.- Energía de flujo o de Presión: Originada por la presión que las moléculas del fluido que actúan entre si, por lo que el trabajo realizado para el desplazamiento de éstas moléculas es igual a la energía ante mencionada.

$\displaystyle {{E}_{flujo}}=P\frac{m}{\rho }$

Hay una deducción matemática que parte del trabajo neto realizado por las moléculas, pero no la explicaremos por ahora, de ser necesaria la incluiremos en los comentarios.

Así, de acuerdo con el teorema de Bernoulli , la suma de las energías de un punto inicial, deberá ser igual a las energías obtenidas en la salida. Entonces matemáticamente tenemos lo siguiente:

$\displaystyle E{{c}_{1}}+E{{p}_{1}}+{{E}_{presion1}}=E{{c}_{2}}+E{{p}_{2}}+{{E}_{presion2}}$

Al sustituir las energías, tenemos que:

$\displaystyle \frac{1}{2}m{{v}_{1}}^{2}+mg{{h}_{1}}+\frac{{{p}_{1}}m}{{{\rho }_{1}}}=\frac{1}{2}m{{v}_{2}}^{2}+mg{{h}_{2}}+\frac{{{p}_{2}}m}{{{\rho }_{2}}}$

Vamos a dividir la ecuación por la masa, ya que es una variable que se repite en todas las expresiones.

$\displaystyle \frac{1}{2}{{v}_{1}}^{2}+g{{h}_{1}}+\frac{{{p}_{1}}}{{{\rho }_{1}}}=\frac{1}{2}{{v}_{2}}^{2}+g{{h}_{2}}+\frac{{{p}_{2}}}{{{\rho }_{2}}}$

Qué vendría a ser la ecuación de Bernoulli, y esta ecuación es aplicable en todos los aspectos de flujo de fluidos, solo que debemos tener en cuenta que la presión P debe tomarse como la presión absoluta y no la presión manométrica, todas las unidades finalmente son en presión.

⛔ Restricciones de la Ecuación de Bernoulli

Aunque la ecuación de Bernoulli se aplica a muchos problemas prácticos, o ejemplos hay ciertas limitaciones que se deben de considerar, a fin de aplicarse con la propiedad adecuada.

1.- Es válida solamente para fluidos incompresibles, ya que el peso específico del fluido permanece constante en la sección inicial y final.
2.- No puede haber sistemas mecánicos que agreguen o retiren energía del sistema entre la sección inicial y final , ya que la energía del sistema permanece constante.
3.- Al igual que el punto dos, no puede haber transferencia de calor hacia el fluido o fuera de éste.
4.- No debe considerarse la pérdida de energía debido a la fricción.

Aunque realmente ningún sistema existente satisface las restricciones, hay muchos sistemas que necesitan de la ecuación de Bernoulli, ya que los errores generados son mínimos.

⭐ Ejercicios Resueltos del Principio de Bernoulli

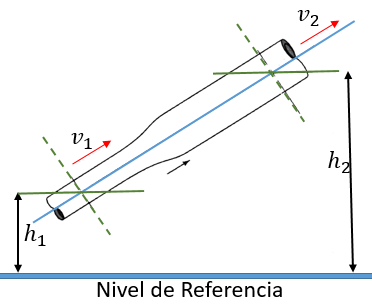
Solución:

Tenemos que analizar nuestros datos, es decir, que es lo qué si tenemos y lo que nos hace falta por encontrar, así también realizar el despeje de la variable que vamos a calcular. Entonces procedemos:

Datos:

d1 = 25 mm

d2 = 50 mm

p1 =345 Kpa

v1 = 3 m/s

d2 = 50 mm

p2  =?

Si leemos bien el problema, nos daremos cuenta que tenemos la altura, ya que si hacemos h2 – h1 = 2 metros. Por lo que nos ahorramos algo de cálculo. Finalmente procedemos a despejar a p2 de la fórmula que ya tenemos:

$\displaystyle \frac{1}{2}{{v}_{1}}^{2}+g{{h}_{1}}+\frac{{{p}_{1}}}{{{\rho }_{1}}}=\frac{1}{2}{{v}_{2}}^{2}+g{{h}_{2}}+\frac{{{p}_{2}}}{{{\rho }_{2}}}$

Despejando y para hacer más fácil el proceso, recordemos que la densidad del agua no tendrá ninguna variación tanto al inicio como al final, entonces podemos decir que la densidad será constante, y la podemos omitir para el cálculo.

$\displaystyle {{p}_{2}}=\frac{1}{2}{{v}_{1}}^{2}-\frac{1}{2}{{v}_{2}}^{2}+g{{h}_{1}}-g{{h}_{2}}+{{p}_{1}}$

Sin embargo nos hace falta v2, ya que no la tenemos, pero si tenemos el dato de los diámetros, entonces si recordamos bien; podemos hacer uso de la ecuación de continuidad  qué es una ecuación que deriva del gasto .

Así que:

$\displaystyle {{A}_{1}}{{v}_{1}}={{A}_{2}}{{v}_{2}}$

Despejando a “v2”

$\displaystyle {{v}_{2}}=\frac{{{A}_{1}}{{v}_{1}}}{{{A}_{2}}}$

Calculando ahora las áreas 1 y 2.

$\displaystyle {{A}_{1}}=\frac{\pi {{d}_{1}}^{2}}{4}=\frac{\pi {{(25mm)}^{2}}}{4}=491m{{m}^{2}}$

La otra área

$\displaystyle {{A}_{2}}=\frac{\pi {{d}_{2}}^{2}}{4}=\frac{\pi {{(50mm)}^{2}}}{4}=1963m{{m}^{2}}$

Ahora de la ecuación de continuidad tenemos que:

$\displaystyle {{v}_{2}}=\frac{{{A}_{1}}{{v}_{1}}}{{{A}_{2}}}=\frac{\left( 491m{{m}^{2}} \right)\left( 3\frac{m}{s} \right)}{1963m{{m}^{2}}}=0.75\frac{m}{s}$

Ahora si podemos utilizar nuestra fórmula despejada de la presión en 2.

$\displaystyle {{p}_{2}}=\frac{1}{2}{{v}_{1}}^{2}-\frac{1}{2}{{v}_{2}}^{2}+g{{h}_{1}}-g{{h}_{2}}+{{p}_{1}}$

Factorizamos un poco… 😎

$\displaystyle {{p}_{2}}=\frac{1}{2}\left( {{v}_{1}}^{2}-{{v}_{2}}^{2} \right)+g\left( {{h}_{1}}-{{h}_{2}} \right)+{{p}_{1}}$

Sustituimos todos nuestros datos

$\displaystyle {{p}_{2}}=\frac{1}{2}\left( {{(3)}^{2}}-{{(0.75)}^{2}} \right)+(9.81)\left( 0-2 \right)+345kPa$

Por lo que el resultado nos da:

$\displaystyle {{p}_{2}}=329.6kPa$

Qué sería la presión en la sección 2, recordemos que ésta información es cierta. Ya que la presión disminuyó.

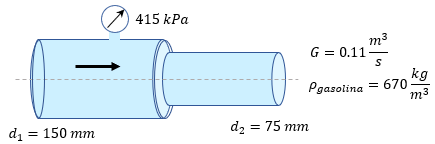
Solución:

A diferencia del problema anterior, podemos observar que están a la misma altura tanto el punto 1 como el punto 2, es decir que no existe ninguna variación por la diferencia de las alturas, observe que se colocó una línea punteada que significa justamente lo que acabamos de explicar. Por lo tanto:

$\displaystyle {{h}_{1}}={{h}_{2}}$

Si esto es así, entonces la ecuación principal de Bernoulli, se tendrá que ver simplificada, de alguna forma, veamos la fórmula original:

$\displaystyle \frac{{{v}_{1}}^{2}}{2}+g{{h}_{1}}+\frac{{{p}_{1}}}{{{\rho }_{1}}}=\frac{{{v}_{2}}^{2}}{2}+g{{h}_{2}}+\frac{{{p}_{2}}}{{{\rho }_{2}}}$

Como hemos dicho, al realizar h1 = h2. Entonces la ecuación se simplifica de esta forma:

$\displaystyle \frac{{{v}_{1}}^{2}}{2}+\frac{{{p}_{1}}}{{{\rho }_{1}}}=\frac{{{v}_{2}}^{2}}{2}+\frac{{{p}_{2}}}{{{\rho }_{2}}}$

Como el problema nos pide calcular a la presión 2, entonces lo despejamos de la fórmula:

$\displaystyle \frac{{{p}_{2}}}{{{\rho }_{2}}}=\frac{{{v}_{1}}^{2}}{2}+\frac{{{p}_{1}}}{{{\rho }_{1}}}-\frac{{{v}_{2}}^{2}}{2}$

$\displaystyle \frac{{{p}_{2}}}{{{\rho }_{2}}}=\frac{{{p}_{1}}}{{{\rho }_{1}}}+\left( \frac{{{v}_{1}}^{2}-{{v}_{2}}^{2}}{2} \right)$

$\displaystyle {{p}_{2}}=\frac{{{p}_{1}}{{\rho }_{2}}}{{{\rho }_{1}}}+{{\rho }_{2}}\left( \frac{{{v}_{1}}^{2}-{{v}_{2}}^{2}}{2} \right)$

Como la densidad 1 y la densidad 2, son las mismas porque se trata de la misma gasolina entonces la podemos simplificar también, quedando así:

$\displaystyle {{p}_{2}}={{p}_{1}}+{{\rho }_{2}}\left( \frac{{{v}_{1}}^{2}-{{v}_{2}}^{2}}{2} \right)$

Ahora si podemos empezar a resolver el ejercicio, porque ya tenemos la fórmula que usaremos:

Datos del problema:

$\displaystyle {{d}_{1}}=150mm\left( \frac{1m}{1000mm} \right)=0.15m$

$\displaystyle {{d}_{2}}=75mm\left( \frac{1m}{1000mm} \right)=0.075m$

$\displaystyle {{p}_{1}}=415kPa$

$\displaystyle G=0.11\frac{{{m}^{3}}}{s}$

$\displaystyle {{\rho }_{gasolina}}=670\frac{kg}{{{m}^{3}}}$

♦ Resolviendo el ejercicio

Si analizamos los datos y la fórmula que utilizaremos, nos hace falta la velocidad inicial y la velocidad final. Para poder obtener la velocidad inicial basta con entender que el Gasto es el producto de la velocidad por el área, y afortunadamente estos datos si los poseemos, entonces tenemos:

$\displaystyle {{Q}_{1}}={{v}_{1}}{{A}_{1}}$

Despejando a la velocidad inicial o velocidad 1

$\displaystyle {{v}_{1}}=\frac{{{Q}_{1}}}{{{A}_{1}}}$

Solamente tenemos el diámetro uno de la primer sección, pero no tenemos el área entonces la calculamos:

$\displaystyle {{v}_{1}}=\frac{{{Q}_{1}}}{{{A}_{1}}}=\frac{0.11\frac{{{m}^{3}}}{s}}{\frac{\pi {{\left( 0.15m \right)}^{2}}}{4}}=6.22\frac{m}{s}$

Para obtener la velocidad final o velocidad 2, aplicamos la ecuación de continuidad.

$\displaystyle {{v}_{1}}{{A}_{1}}={{v}_{2}}{{A}_{2}}$

Despejando a la velocidad 2

$\displaystyle {{v}_{2}}=\frac{{{v}_{1}}{{A}_{1}}}{{{A}_{2}}}$

Pero sabemos también que si multiplicamos la velocidad 1 con el área 1, lógicamente obtendremos el Gasto que nos da el problema, es decir:

$\displaystyle {{v}_{2}}=\frac{{{v}_{1}}{{A}_{1}}}{{{A}_{2}}}=\frac{{{G}_{1}}}{{{A}_{2}}}$

$\displaystyle {{v}_{2}}=\frac{{{G}_{1}}}{{{A}_{2}}}$

Entonces podemos sustituir nuestros datos, para obtener la velocidad 2

$\displaystyle {{v}_{2}}=\frac{{{G}_{1}}}{{{A}_{2}}}=\frac{0.11\frac{{{m}^{3}}}{2}}{\frac{\pi {{\left( 0.075m \right)}^{2}}}{4}}=24.9\frac{m}{s}$

Ahora que ya tenemos tanto a la velocidad 1, como la velocidad 2. Podemos sustituir los datos en la fórmula para obtener la presión 2, que es lo que nos pide el problema:

$\displaystyle {{p}_{2}}=415kPa+670\frac{kg}{{{m}^{3}}}\left( \frac{{{\left( 6.22\frac{m}{s} \right)}^{2}}-{{\left( 24.9\frac{m}{s} \right)}^{2}}}{2} \right)$

$\displaystyle {{p}_{2}}=415kPa+670\frac{kg}{{{m}^{3}}}\left( \frac{-581.3216}{2} \right)$

$\displaystyle {{p}_{2}}=415kPa+670\frac{kg}{{{m}^{3}}}\left( -290.6608 \right)$

$\displaystyle {{p}_{2}}=415kPa-194742.74Pa$

Aplicando la resta:

$\displaystyle {{p}_{2}}=220257.26Pa=220.26kPa$

Que vendría a ser nuestro resultado 220.26kPa

🔱 Aplicación de la Ecuación de Bernoulli

Existen dos grandes aplicaciones del principio de Bernoulli, entre ellas está el Principio o Teorema de Torricelli y el tubo de Venturi. Por ahora daremos una breve reseña ya que si quieres aprender a resolver ejercicios de ambos temas, tendrás que ir al artículo de cada estudio.

👉 Teorema de Torricelli

Es una de las aplicaciones del teorema de Bernoulli, que se tiene cuando se desea encontrar la magnitud de velocidad de salida que tiene un líquido a través de algún orificio de cualquier recipiente.

👉 Tubo de Venturi

El tubo de Venturi se emplea para calcular la velocidad de un líquido que circula a presión dentro de una tubería. Su funcionamiento está fundamentado en el teorema de Bernoulli.

📃 Ejercicios para Practicar del Principio de Bernoulli

Ahora es momento de practicar los ejercicios del principio de Bernoulli, esto es muy importante para aprender a dominar mucho mejor el tema 😊👇

👉 Ver Solución

👉 Ver Solución

• Comparte este artículo:
• Twittear