Teorema de Torricelli - Ejercicios Resueltos

Eyy!! ¿Cómo están lectores?, seguimos en nuestro labor de publicar artículos para ustedes y lógicamente anexar ejercicios resueltos para mejorar el entendimiento de cada tema, pues bien en esta ocasión hablaremos de otra de las grandes aplicaciones que se derivan del principio de bernoulli , y que en Física es importante conocer, pues muchos experimentos básicos parten de este principio. El gran Teorema de Torricelli o también llamado como el Principio de Torricelli 😎

Evangelista Torricelli nació en Faenza, Italia por el año 1608. Fue un físico y matemático muy reconocido en esa época, es acreedor del descubrimiento del barómetro de mercurio, y que en honor a su nombre existe una unidad de presión llamada "torr"equivalente a un milimetro de mercurio (mm de Hg).

🤔 ¿Qué es el Teorema de Torricelli?

Pues bien, el Teorema de Torricelli es un fenómeno que ocurre a la salida de un liquido por un orificio que posee algún recipiente que lo contiene. La superficie de la sección horizontal del recipiente suele ser bastante grande, en relación con la del agujero, para que pueda despreciarse la velocidad a la que desciende la superficie libre del líquido. En esas condiciones puede demostrarse fácilmente que, a la salida del orificio, el líquido adquiere una velocidad que es precisamente la misma que si cayese en efecto de la gravedad, o sea libremente desde el nivel de la superficie libre al nivel del agujero. Pero bueno, esto puede ser confuso, lo veamos gráficamente.

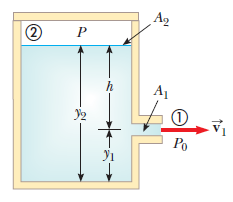
Imaginemos que deseamos encontrar la velocidad de salida de un líquido a través de un orificio en un recipiente. Para ello, tenemos que recurrir a la fórmula conocida de Bernoulli.

🔸 Deducción de la fórmula de Torricelli

De la imagen anterior podemos observar a la presión, a la altura, al área y la velocidad, entonces de nuestra fórmula de Bernoulli tenemos que:

$\displaystyle \frac{{{v}_{1}}^{2}}{2}+g{{h}_{1}}+\frac{{{p}_{1}}}{{{\rho }_{1}}}=\frac{{{v}_{2}}^{2}}{2}+g{{h}_{2}}+\frac{{{p}_{2}}}{{{\rho }_{2}}}$

Vamos a proceder a suprimir a la energía cinética del punto 2, puesto que la velocidad del líquido en el punto 2 es despreciable si la comparamos con la magnitud de velocidad de salida en el punto 1. Así que;

$\displaystyle \frac{{{v}_{1}}^{2}}{2}+g{{h}_{1}}+\frac{{{p}_{1}}}{{{\rho }_{1}}}=g{{h}_{2}}+\frac{{{p}_{2}}}{{{\rho }_{2}}}$

Como en el punto 1 se encuentre en el fondo del recipiente, a una altura cero sobre la superficie, entonces podemos eliminar el término o sea que la energía potencial en el punto 1, no debemos considerarla.

$\displaystyle \frac{{{v}_{1}}^{2}}{2}+\frac{{{p}_{1}}}{{{\rho }_{1}}}=g{{h}_{2}}+\frac{{{p}_{2}}}{{{\rho }_{2}}}$

Como la energía de presión es provocada por la presión atmosférica y ésta es la misma en los dos puntos, entonces decimos que:

$\displaystyle \frac{{{v}_{1}}^{2}}{2}=g{{h}_{2}}$

Despejando a la velocidad, tenemos que:

$\displaystyle {{v}_{1}}=\sqrt{2g{{h}_{2}}}$

Generalizando esto es:

$\displaystyle v=\sqrt{2gh}$

Dónde:

v = Velocidad del líquido que sale por el orificio (m/s)

g = Magnitud de la aceleración de la gravedad (9.8 m/s^2)

h = profundidad a la que se encuentra el orificio de salida (m)

🔹 Fórmula del Teorema de Torricelli

En conclusión la fórmula del teorema de Torricelli es la siguiente:

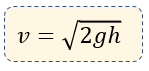
Ejercicios Resueltos del Teorema de Torricelli

Solución:

Analizando el problema y considerando nuestros datos, tenemos que:

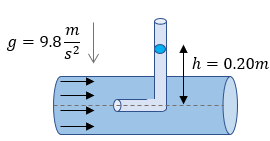
v = ?

h = 1.4 m

g = 9.8 m/s^2

Aplicando la fórmula:

$\displaystyle v=\sqrt{2gh}=\sqrt{2(9.8\frac{m}{{{s}^{2}}})(1.4m)}=\sqrt{27.44}=5.24\frac{m}{s}$

Veamos otro ejemplo:

Solución: 

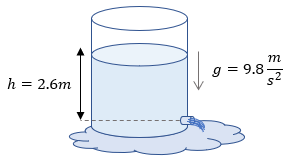
Bien, para poder resolver este ejemplo, simplemente tenemos que despejar a la variable "h" de nuestra fórmula:

$\displaystyle h=\frac{{{v}^{2}}}{2g}$

Sustituyendo nuestros datos que son:

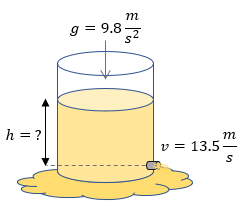
v = 9 m/s

g = 9.8 m/s^2

$\displaystyle h=\frac{{{v}^{2}}}{2g}=\frac{{{(9\frac{m}{s})}^{2}}}{2(9.8\frac{m}{{{s}^{2}}})}=4.13m$

Que vendría a ser nuestro resultado.

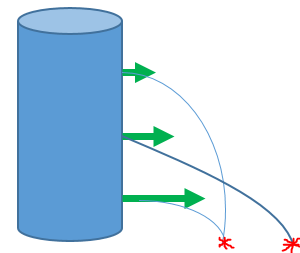
Con estos ejercicios hemos demostrado que la Ley de Torricelli no es difícil en absoluto, simplemente tenemos que aplicar nuestra fórmula. Pero, hay cosas más interesantes todavía, por ejemplo la velocidad de descarga aumenta con la profundidad. Aunque el alcance máximo se logra cuando el orificio se encuentra a la mitad del nivel del agua.

Espero que te haya servido estos ejercicios, si tienes dudas al respecto, favor de dejarlo en la caja de comentarios puestas aquí abajo!! 😀

📃 Ejercicios para Practicar del Teorema de Torricelli

A partir de ahora hemos colocado algunos ejemplos resueltos paso a paso sobre el teorema de torricelli, es muy probable que tengas dudas y se tratará de aclarar todo en los ejemplos resueltos, recuerda dar click en "ver solución".

👉 Ver Solución

👉 Ver Solución

👉 Ver Solución