Tiro horizontal - Ejercicios Resueltos

¿Cómo están lectores? 😎 Anteriormente a esta publicación hablamos sobre el tiro parabólico, y explicamos las diversas fórmulas, con ejercicios resueltos paso a paso, para que cada lector de Fisimat entienda perfectamente de que trata el tema, así que hoy nos toca hablar sobre el tiro horizontal o lanzamiento horizontal, el cuál lo explicaremos más práctico que teórico puesto que todo parte del movimiento parabólico, así que presta mucha atención, porque tenemos que definir el término de movimiento horizontal.
Entonces ¿qué es el tiro horizontal? el tiro horizontal es aquél movimiento que se caracteriza por describir un camino curvo que sigue un cuerpo al ser lanzando horizontalmente, es el resultado de dos movimientos independientes; un movimiento horizontal con velocidad constante y otro vertical, la diferencia de éste movimiento con el tiro parabólico es que al inicio del movimiento el proyectil solo posee una velocidad horizontal (vx), debido a que carece de ángulo de inclinación, , por lo tanto no presente velocidad vertical inicial , o sea que (vy = 0), para entender un poco mejor el movimiento, veamos la siguiente imagen.
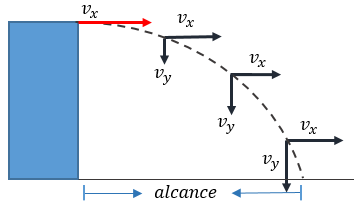
Las ecuaciones del tiro horizontal son similares al del movimiento parabólico, teniendo en cuenta que no hay velocidad inicial en "y".
Fórmulas del Tiro Horizontal
No necesitamos aprendernos muchas fórmulas, es muy sencillo. Solo debemos de tener en cuenta las siguientes:
1.- Para realizar los cálculos de las velocidades iniciales.
$\displaystyle {{v}_{x}}={{v}_{0x}}$
$\displaystyle {{v}_{0y}}=0$
Con esto observamos, que solamente al inicio tenemos velocidad inicial en "x", y en "y" es prácticamente nulo.
2.- Para calcular la posición horizontal y vertical en cualquier instante.
$\displaystyle x=\left( {{v}_{0x}} \right)\left( t \right)$
$\displaystyle y=\frac{\left( g \right)\left( {{t}^{2}} \right)}{2}$
3.- Para calcular las componentes de la velocidad "v" en cualquier instante.
$\displaystyle {{v}_{0x}}={{v}_{x}}$
$\displaystyle {{v}_{y}}=\left( g \right)\left( t \right)$
Si observamos, solamente tenemos que calcular la velocidad en "y" , porque la de "x" es la misma que la inicial.
4.- Para poder calcular la velocidad en cualquier instante aplicamos la siguiente fórmula:
$\displaystyle v=\sqrt{{{\left( {{v}_{x}} \right)}^{2}}+{{\left( {{v}_{y}} \right)}^{2}}}$
5.- Para poder calcular el tiempo que permanece en el aire el objeto, aplicamos:
$ \displaystyle t=\sqrt{\frac{2\left( y \right)}{g}}$
Bien, ahora es momento perfecto para practicar. Así que poner atención a los problemas para no tener dudas.
Ejercicios Resueltos del Tiro Horizontal
Vamos con el primer ejemplo.
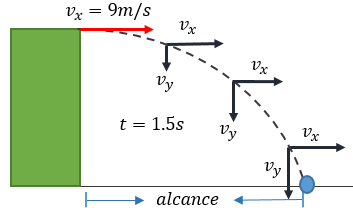
Solución: Recordemos que al ser un tiro horizontal, la velocidad vertical no existe, solo tendremos una velocidad inicial en "x" que es de 9 m/s, ahora si nos piden calcular la distancia horizontal y vertical, en determinado tiempo, podemos recurrir a la fórmula 2.
Así que para nuestra posición en "x", aplicamos:
$\displaystyle x=\left( {{v}_{0x}} \right)\left( t \right)=\left( 9\frac{m}{s} \right)\left( 1.5s \right)=13.5m$
Ahora aplicando la fórmula de "y", tenemos:
$\displaystyle y=\frac{\left( g \right)\left( {{t}^{2}} \right)}{2}=\frac{\left( 9.8\frac{m}{{{s}^{2}}} \right){{\left( 1.5s \right)}^{2}}}{2}=11.025m$
Por lo que (13.5 m, 11.025m) son las coordenadas de posición donde ha descendido la pelota. Problema resuelto 😎
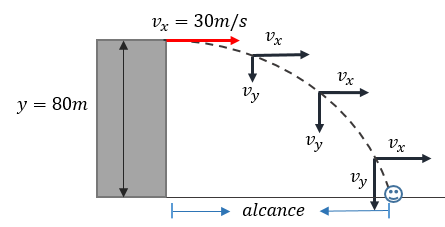
Solución: Bien, nuevamente seguiremos haciendo uso de nuestras fórmulas para la solución de éste problema, así que prestad atención.
a) Para calcular cuanto tiempo permanece en el aire, aplicaremos la fórmula 5:
$\displaystyle t=\sqrt{\frac{2\left( y \right)}{g}}=\sqrt{\frac{2\left( 80m \right)}{9.8\frac{m}{{{s}^{2}}}}}=4.04s$
Qué sería el tiempo que el esquiador permanece en el aire.
b) Para poder saber lo lejos que viajó horizontalmente, aplicamos la fórmula de la posición en "x".
$\displaystyle x=\left( {{v}_{0x}} \right)\left( t \right)=\left( 30\frac{m}{s} \right)\left( 4.04s \right)=121.2m$
c) Para calcular las componentes de velocidad horizontal y vertical.
Como se trata de un tiro horizontal, la velocidad horizontal es la misma que la inicial , es decir. 30m/s, la única que nos haría falta sería la velocidad vertical , así que aplicamos.
$\displaystyle {{v}_{y}}=\left( g \right)\left( t \right)=\left( 9.8\frac{m}{{{s}^{2}}} \right)\left( 4.04s \right)=39.6\frac{m}{s}$
y listo, problema resuelto 😀
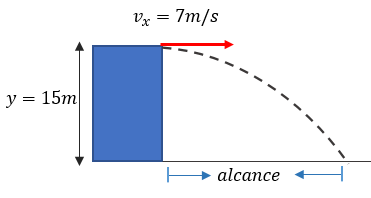
Solución: Nuevamente aplicaremos las fórmulas antes mencionadas, solo que ésta vez lo haremos más intuitivamente.
a) Para poder calcular el tiempo de caída apliquemos:
$\displaystyle t=\sqrt{\frac{2\left( y \right)}{g}}=\sqrt{\frac{2\left( 15m \right)}{9.8\frac{m}{{{s}^{2}}}}}=1.75s$
b) Para poder calcular la distancia de la base del edificio aplicamos:
$\displaystyle x=\left( {{v}_{0x}} \right)\left( t \right)=\left( 7\frac{m}{s} \right)\left( 1.75s \right)=12.25m$
c) Para obtener las componentes horizontal y vertical de velocidad aplicamos lo siguiente:
$\displaystyle {{v}_{x}}=7\frac{m}{s}$
La velocidad horizontal, es la misma que la inicial.
$\displaystyle {{v}_{y}}=\left( g \right)\left( t \right)=\left( 9.8\frac{m}{{{s}^{2}}} \right)\left( 1.75s \right)=17.15\frac{m}{s}$
Conclusión
El tiro horizontal representa uno de los temas en dos dimensiones muy importantes en Física, es de gran interés estudiar para ver lo que ocurre con los proyectiles, su alcance, su velocidad final, el vector velocidad al momento de caer, entre otras características involucradas en el movimiento. ¿te gustó el tema? , no dudes en compartir 😀
-
Me pueden ayudar con un ejercicio
Un monomotor vuela horizontalmente con una rapidez de 100 m/s a 500m de altura y suelta una esfera de plomo de 20 kilogramos de masa. Cual Es el tiempo que tardara la esfera en tocar el piso-
Es cierto lo he calculado y me da lo mismo?
-
-
En el primer ejercicio se supone que la gravedad (g) es negativa, entonces el resultado para (y) es negativo;
seria -11.025 y no 11.025-
En física, la dirección del vector es la que da la negatividad o la positividad, no la fórmula matemática
-
-
pregunto ejercicios no problemas de matemáticas
-
Pregunta, cuando en un ejercicio me dice que calculé el punto donde llegará el balón al suelo, primero tengo que sacar el tiempo que tarda y después encontrar la distancia?
-
Porque en el problema 2 en el punto a) el resultado te dio 4.04, si cuando hago la operación me da 11.5
-
seguro pusiste todo directo en la calculadora, primero has la multiplicacion 2(80) luego la division y a tu resultado le sacas raiz
-
Ayúdenme a resolver este problema x favor: desde una Azotea de 490 mts se lanza horizontalmente un proyectil. No tomando en cuenta la resistencia del aire, si el alcance horizontal es 145m, Calcular: con que velocidad se lanzó? B) Módulo de la velocidad final del proyectil
-
Revisa los datos escritos
t=√2.80m/9,8 m/seg•=-
Por favor Me podrian ayudar a resolver estos problemas: una pala se dispara horizontalmente desde una altura de 50 metros, con una velocidad inicial de 30m/s. Hayar
A.velocidad a los 3seg
B.direccion de la velocidad
C. AlcanceDesde el suelo se patea un balon con una velocidad de 70m/s y un angulo de 50grados. Hayar
A tiempo de vuelo
B. Altura maxima
C. Velocidad a los 5seg
Direccion de la velocidad
E. Alcance
-
-
Calcula el tiempo de vuelo: tv = 2y/g ; y luego sacas la raíz cuadrada. El resultado es 10 seg. Luego utiliza la ecuación del alcance horizontal: X = Vox . tv ; despeja Vox = X / tv. El resultado es 14,5 m/s
-
-
-
Por qué tienes que sacar raíz
-
una pelota rueda por una mesa horizontal de una altura de 1,22m y llega al suelo a una distancia 1,52m de borde de mesa ¿ con que velocidad salió disparada de la mesa ?
-
asi indica la formula xd
-
-
Multiplica 2x80=160. Divide 160 para 9.8 160÷9.8=16.33 ahora sacale la raíz cuadrada de 16.33=4.04 y listo
-
amigo porque tienes que multiplicar el 2.80m/s = 160m/s y dividir con 9.8m/s2 dando como resultado 16,32s y en raiz seria 4,04 queda en segundo porque 1 metro diviendo y y metro multiplicando se cancelan igual que el segundo , pero el segundo estab al cuadrado
-
2 X 80 metros / 9,8 m/s = 16,32653061 se extrae raíz cuadrada de esa cantidad = 4,040610178
Saludos -
Sí
-
2x80=160
160÷9.8=16,32
✓16,32=4,04 -
2x80=160/9.8=16.32
Se le saca raíz cuadrada u da 4. 04. -
Hola, en el punto 2 si da 4,04 por que multiplica 2 * 80m = 160m luego se divide 160/ 9,8m/s= 16.326 luego se le saca la raiz a 16.326 = 4,04
-
por la forma en ingresar la información en la calculadora, para no tener inconvenientes primero 2*80=160, luego dividimos 160/9.8 = 16.326 y por último se obtiene la raíz cuadrada t = 4.04 segundos.
-
48 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar