Tiro horizontal - Ejercicios Resueltos

¿Cómo están lectores? 😎 Anteriormente a esta publicación hablamos sobre el tiro parabólico, y explicamos las diversas fórmulas, con ejercicios resueltos paso a paso, para que cada lector de Fisimat entienda perfectamente de que trata el tema, así que hoy nos toca hablar sobre el tiro horizontal o lanzamiento horizontal, el cuál lo explicaremos más práctico que teórico puesto que todo parte del movimiento parabólico, así que presta mucha atención, porque tenemos que definir el término de movimiento horizontal.
Entonces ¿qué es el tiro horizontal? el tiro horizontal es aquél movimiento que se caracteriza por describir un camino curvo que sigue un cuerpo al ser lanzando horizontalmente, es el resultado de dos movimientos independientes; un movimiento horizontal con velocidad constante y otro vertical, la diferencia de éste movimiento con el tiro parabólico es que al inicio del movimiento el proyectil solo posee una velocidad horizontal (vx), debido a que carece de ángulo de inclinación, , por lo tanto no presente velocidad vertical inicial , o sea que (vy = 0), para entender un poco mejor el movimiento, veamos la siguiente imagen.
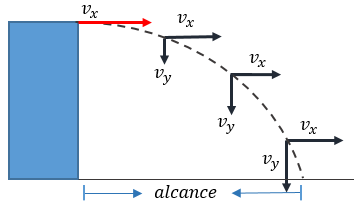
Las ecuaciones del tiro horizontal son similares al del movimiento parabólico, teniendo en cuenta que no hay velocidad inicial en "y".
Fórmulas del Tiro Horizontal
No necesitamos aprendernos muchas fórmulas, es muy sencillo. Solo debemos de tener en cuenta las siguientes:
1.- Para realizar los cálculos de las velocidades iniciales.
$\displaystyle {{v}_{x}}={{v}_{0x}}$
$\displaystyle {{v}_{0y}}=0$
Con esto observamos, que solamente al inicio tenemos velocidad inicial en "x", y en "y" es prácticamente nulo.
2.- Para calcular la posición horizontal y vertical en cualquier instante.
$\displaystyle x=\left( {{v}_{0x}} \right)\left( t \right)$
$\displaystyle y=\frac{\left( g \right)\left( {{t}^{2}} \right)}{2}$
3.- Para calcular las componentes de la velocidad "v" en cualquier instante.
$\displaystyle {{v}_{0x}}={{v}_{x}}$
$\displaystyle {{v}_{y}}=\left( g \right)\left( t \right)$
Si observamos, solamente tenemos que calcular la velocidad en "y" , porque la de "x" es la misma que la inicial.
4.- Para poder calcular la velocidad en cualquier instante aplicamos la siguiente fórmula:
$\displaystyle v=\sqrt{{{\left( {{v}_{x}} \right)}^{2}}+{{\left( {{v}_{y}} \right)}^{2}}}$
5.- Para poder calcular el tiempo que permanece en el aire el objeto, aplicamos:
$ \displaystyle t=\sqrt{\frac{2\left( y \right)}{g}}$
Bien, ahora es momento perfecto para practicar. Así que poner atención a los problemas para no tener dudas.
Ejercicios Resueltos del Tiro Horizontal
Vamos con el primer ejemplo.
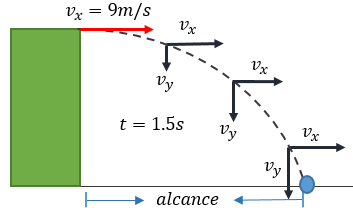
Solución: Recordemos que al ser un tiro horizontal, la velocidad vertical no existe, solo tendremos una velocidad inicial en "x" que es de 9 m/s, ahora si nos piden calcular la distancia horizontal y vertical, en determinado tiempo, podemos recurrir a la fórmula 2.
Así que para nuestra posición en "x", aplicamos:
$\displaystyle x=\left( {{v}_{0x}} \right)\left( t \right)=\left( 9\frac{m}{s} \right)\left( 1.5s \right)=13.5m$
Ahora aplicando la fórmula de "y", tenemos:
$\displaystyle y=\frac{\left( g \right)\left( {{t}^{2}} \right)}{2}=\frac{\left( 9.8\frac{m}{{{s}^{2}}} \right){{\left( 1.5s \right)}^{2}}}{2}=11.025m$
Por lo que (13.5 m, 11.025m) son las coordenadas de posición donde ha descendido la pelota. Problema resuelto 😎
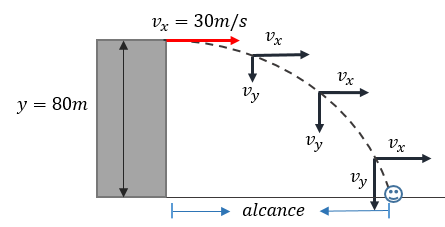
Solución: Bien, nuevamente seguiremos haciendo uso de nuestras fórmulas para la solución de éste problema, así que prestad atención.
a) Para calcular cuanto tiempo permanece en el aire, aplicaremos la fórmula 5:
$\displaystyle t=\sqrt{\frac{2\left( y \right)}{g}}=\sqrt{\frac{2\left( 80m \right)}{9.8\frac{m}{{{s}^{2}}}}}=4.04s$
Qué sería el tiempo que el esquiador permanece en el aire.
b) Para poder saber lo lejos que viajó horizontalmente, aplicamos la fórmula de la posición en "x".
$\displaystyle x=\left( {{v}_{0x}} \right)\left( t \right)=\left( 30\frac{m}{s} \right)\left( 4.04s \right)=121.2m$
c) Para calcular las componentes de velocidad horizontal y vertical.
Como se trata de un tiro horizontal, la velocidad horizontal es la misma que la inicial , es decir. 30m/s, la única que nos haría falta sería la velocidad vertical , así que aplicamos.
$\displaystyle {{v}_{y}}=\left( g \right)\left( t \right)=\left( 9.8\frac{m}{{{s}^{2}}} \right)\left( 4.04s \right)=39.6\frac{m}{s}$
y listo, problema resuelto 😀
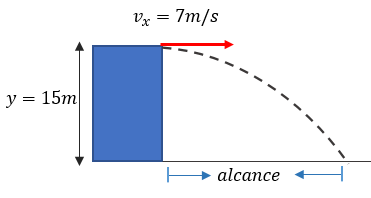
Solución: Nuevamente aplicaremos las fórmulas antes mencionadas, solo que ésta vez lo haremos más intuitivamente.
a) Para poder calcular el tiempo de caída apliquemos:
$\displaystyle t=\sqrt{\frac{2\left( y \right)}{g}}=\sqrt{\frac{2\left( 15m \right)}{9.8\frac{m}{{{s}^{2}}}}}=1.75s$
b) Para poder calcular la distancia de la base del edificio aplicamos:
$\displaystyle x=\left( {{v}_{0x}} \right)\left( t \right)=\left( 7\frac{m}{s} \right)\left( 1.75s \right)=12.25m$
c) Para obtener las componentes horizontal y vertical de velocidad aplicamos lo siguiente:
$\displaystyle {{v}_{x}}=7\frac{m}{s}$
La velocidad horizontal, es la misma que la inicial.
$\displaystyle {{v}_{y}}=\left( g \right)\left( t \right)=\left( 9.8\frac{m}{{{s}^{2}}} \right)\left( 1.75s \right)=17.15\frac{m}{s}$
Conclusión
El tiro horizontal representa uno de los temas en dos dimensiones muy importantes en Física, es de gran interés estudiar para ver lo que ocurre con los proyectiles, su alcance, su velocidad final, el vector velocidad al momento de caer, entre otras características involucradas en el movimiento. ¿te gustó el tema? , no dudes en compartir 😀
-
Aqui solo importa la distancia, todo lo demas es irrelevante, con la fórmula y=1/2at^2 y despejas que es, t=(2*500/9.8)^1/2
t=10.10s -
necesito ayuda con este ejercicio
desde una altura de 500m se dispara una bala horizontalmente con una rapidez de 50m/sg calcular:
a)el tiempo total del vuelo b)el alcance-
a) 10,09s b)504,5m
-
-
Por qué en el problema número 3, apartado c, el resultado os ha dado 17.05 si a través de la Fórmula que usted/ es habéis puesto nos ha dado 17.15m/seg.
Calculenlo: Vy=g×t
Vy=9.8×1.75=17.15m/seg -
Por qué en el problema número 3, el apartado C da como resultado 17.05 si a nosotras nos a dado 17.15. Si usted/es quieren pueden verificarlo con vuestros resultados, habéis multiplicado mal.
Ya que la fórmula es como habéis puesto Vy=g×t
Vy=9.8×1.75= 17.15m/seg-
Teneis razón yo tambien lo he calculado y me ha dado lo mismo?
-
-
La formula del segundo problema esta mal. Hay 3 formulas para tiempo: t(subir)= -vo/g t(aire)= -2vo/g
y por ultima t(caer)= raiz de(2h/g)
Favor de arreglar el resultado y la formula ya que yo entre a estudiar y termine revuelto-
En física, la dirección del vector es la que da la negatividad o la positividad, no la fórmula matemática
-
48 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar