Tiro Vertical - Ejercicios Resueltos

El tiro vertical en física es el hecho del movimiento provocado a un cuerpo que está sujeto a desplazarse en línea recta, de manera vertica, ya sea para arriba o para abajo. Algunos físicos lo clasifican en dos tipos de tiros verticales, el tiro vertical ascendente y el tiro vertical descendente.

El tiro vertical ascendente es aquel en el que se lanza un cuerpo hacia arriba, al iniciar este movimiento, el cuerpo adquiere una velocidad máxima, partiendo desde el punto inicial de lanzamiento, posteriormente en su trayectoria por el aire, la aceleración de la gravedad empieza a constrarrestar el movimiento, frenando poco a poco el objeto, con una aceleración negativa de 9.8 m/s². Dado este fenómeno, va a haber un momento en el que el objeto se encuentre totalmente desacelerado.

Al llegar a una velocidad vertical de 0 m/s, el objeto se quedará inmovil en el aire por un instante, para empezar a ser afectado inmediatamente por la aceleración de la gravedad, ahora si en un sentido positivo, experimentando una caída libre.

Fórmulas del Tiro Vertical

Es momento de estudiar las fórmulas que usaremos en este artículo de tiro vertical para tener conocimientos de su uso.

Fórmula para la velocidad inicial

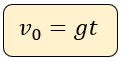
y la siguiente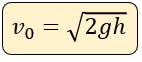

Hay dos fórmulas posibles para calcular la velocidad inicial con la que fue lanzado el objeto. Cualquiera de las dos se pueden utilizar siempre y cuando observemos los valores iniciales que piden, en uno hay tiempo y en otro hay altura.

Fórmula para el tiempo que tarda en alcanzar la altura máxima

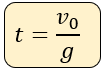
Para este caso, se usa la siguiente fórmula, es muy útil para calcular el tiempo que le toma para llegar hasta arriba.

Fórmula para obtener la altura máxima

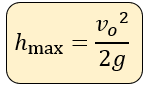
La altura máxima la podemos obtener aplicando la siguiente fórmula, observe que solo necesitamos de la velocidad inicial y la gravedad.

Fórmula para otbener la altura

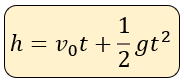
Aunque esta fórmula es aplicable también para la altura máxima, es muy útil para aplicarla en casos que veremos más adelante en ejercicios:

Ejemplos Resueltos de Tiro Vertical

Veamos algunos ejercicios resueltos paso a paso de Tiro Vertical

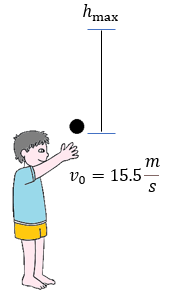
Solución:

Dado que los únicos datos que tenemos para el problema son la velocidad inicial y la gravedad, entonces buscamos la fórmula que más se acople a nuestras necesidades.

$\displaystyle {{v}_{0}}=15\frac{m}{s}$

$\displaystyle g=9.8\frac{m}{{{{s}^{2}}}}$

Empleamos la siguiente fórmula:

$\displaystyle {{h}_{{\max }}}=\frac{{{{v}_{0}}^{2}}}{{2g}}=\frac{{{{{\left( {15\frac{m}{s}} \right)}}^{2}}}}{{2\left( {9.8\frac{m}{{{{s}^{2}}}}} \right)}}=11.48m$

Por lo que la altura máxima que alcanza la piedra es de 11.48 m.

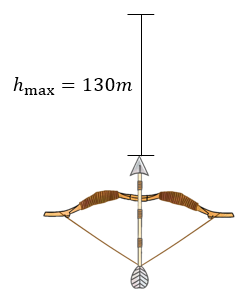
Solución:

Colocamos los datos que tenemos en este ejercicio.

$\displaystyle {{h}_{{\max }}}=130m$

$\displaystyle g=9.8\frac{m}{{{{s}^{2}}}}$

La única fórmula de velocidad inicial que podemos utilizar, es la fórmula que no tiene implícita el tiempo, sino la que tiene a la altura.

$\displaystyle {{v}_{0}}=\sqrt{{2gh}}=\sqrt{{2(9.8)(130)}}=50.47\frac{m}{s}$

Por lo que la velocidad inicial es de 50.47 m/s

Solución:

Los datos que tenemos ahora del problema anterior, es tanto la velocidad inicial (que recién calculamos), la altura y la gravedad, es decir:

$\displaystyle {{v}_{0}}=50.47\frac{m}{s}$

$\displaystyle h=130m$

$\displaystyle g=9.8\frac{m}{{{{s}^{2}}}}$

Sin embargo, para poder obtener el tiempo que le tomará a la flecha llegar a la parte más alta, la podemos calcular con la siguiente fórmula:

$\displaystyle t=\frac{{{{v}_{0}}}}{g}=\frac{{50.47\frac{m}{s}}}{{9.8\frac{m}{{{{s}^{2}}}}}}=5.15s$

Por lo que obtenemos que el tiempo para alcanzar la altura máxima debe de ser de 5.15 s.

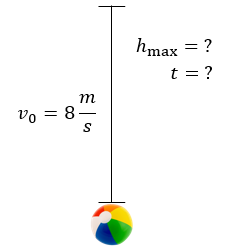
Solución:

Anotamos los datos que tenemos para este ejercicio:

$\displaystyle {{v}_{0}}=8\frac{m}{s}$

$\displaystyle g=9.8\frac{m}{{{{s}^{2}}}}$

Para poder calcular la altura máxima tenemos que emplear la fórmula que ya conocemos:

$\displaystyle {{h}_{{\max }}}=\frac{{{{v}_{0}}^{2}}}{{2g}}=\frac{{{{{\left( {8\frac{m}{s}} \right)}}^{2}}}}{{2\left( {9.8\frac{m}{{{{s}^{2}}}}} \right)}}=3.27m$

Lo que nos da una altura de 3.27 m.

Ahora para poder calcular el tiempo que demora en alcanzar esa altura, lo haremos mediante la siguiente fórmula:

$\displaystyle t=\frac{{{{v}_{0}}}}{g}=\frac{{8\frac{m}{s}}}{{9.8\frac{m}{{{{s}^{2}}}}}}=0.816s$

Por lo que el tiempo que le demoró en alcanzar la altura máxima fue de 0.816 s.

Solución:

En este problema se experimenta un caso diferente, pues habla del tiempo que le demorará al cuerpo en llegar al suelo si se lanza hacia arriba, es decir tenemos que tomar en cuenta dos tiempos, el tiempo que tarda en subir como el tiempo que tarda en bajar. Por lo general para estos problemas al tiempo se le termina multiplicando por 2, esto es debido a que el tiempo de subida es el mismo que el tiempo de bajada. 

Entonces anotamos nuestros datos:

$\displaystyle {{v}_{0}}=30\frac{m}{s}$

$\displaystyle g=9.8\frac{m}{{{{s}^{2}}}}$

Con estos datos, podemos resolver el problema con la siguiente fórmula:

$\displaystyle t=\frac{{{{v}_{0}}}}{g}=\frac{{30\frac{m}{s}}}{{9.8\frac{m}{{{{s}^{2}}}}}}=3.06s$

Obtenemos el tiempo de subida, ahora multiplicándolo por dos obtendremos el total.

$\displaystyle {{t}_{t}}=2\left( {3.06s} \right)=6.12s$

Lo que es un total de 6.12 s.

Ejercicios para practicar de Tiro Vertical