Trabajo Mecánico - Ejercicios Resueltos
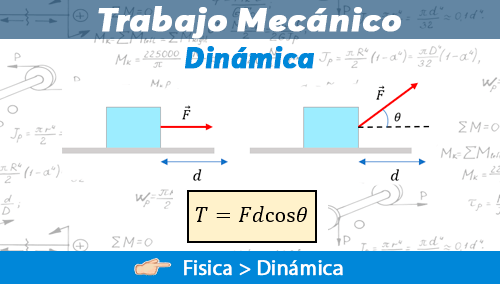
El concepto del trabajo es un concepto muy importante en Física, pero especialmente en el área de Dinámica. Es algo común escuchar "trabajo" en nuestro día a día, y a pesar de que está relacionado con la energía, el trabajo es un esfuerzo qué realizamos todos para llevar a cabo alguna actividad. Para la Física es lo siguiente.
? ¿Qué es el Trabajo en Física?
Vamos a determinar este concepto de la siguiente manera:
? ¿Cuál es la fórmula del Trabajo?
El valor del trabajo se suele calcular multiplicando la magnitud de la componente de la fuerza localizada en la misma dirección en que se efectúa el movimiento por la magnitud del desplazamiento que ésta ha realizado. Matemáticamente lo veríamos de la siguiente forma:
![]()
Dónde:
T = Trabajo Realizado (Nm) = Joules = J
F = Magnitud de la fuerza en dirección del movimiento (N)
d = Magnitud del desplazamiento (m)
Si la fuerza que mueve el cuerpo se encuentra con una inclinación en la dirección donde se efectúa el desplazamiento, tendríamos un ángulo "θ" y la fórmula se vería de la siguiente manera.
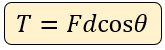
✅ Tipos de Trabajo (Según el ángulo de aplicación)
Trabajo Motor o Positivo
El trabajo motor o trabajo positivo ocurre cuando la fuerza F actúa en la dirección que favorece el movimiento, es decir, cuando el ángulo θ es nulo o forma un ángulo agudo.
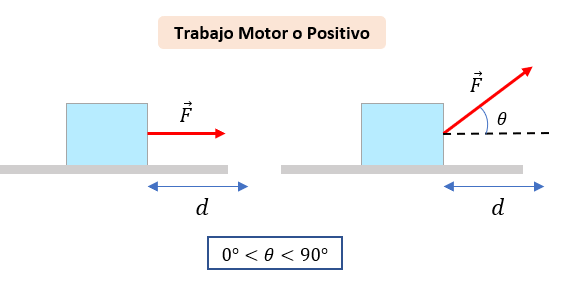
Trabajo Negativo o Resistente
El trabajo negativo o resistente es aquél trabajo donde la fuerza actúa en la dirección opuesta a dicho movimiento, es decir, cuando el ángulo θ forma un ángulo obtuso. o de 180°.
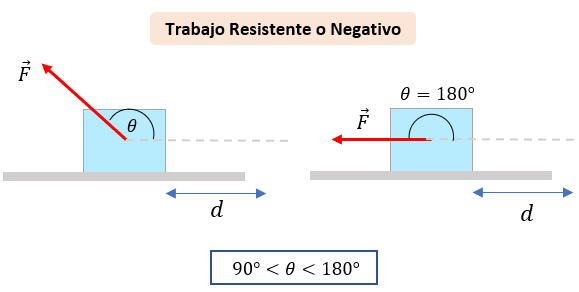
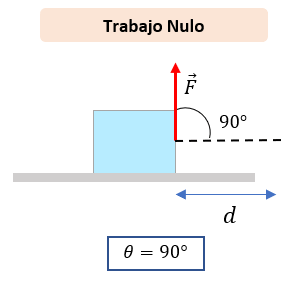
Trabajo Nulo
Se le conoce como trabajo nulo aquél trabajo donde la fuerza y el ángulo de desplazamiento forman un ángulo recto o de 90°. Es decir, cuando el vector fuerza es perpendicular al desplazamiento.
? Ejercicios Resueltos de Trabajo Mecánico
Para entender mejor el tema, veamos algunos ejemplos o problemas de Trabajo Mecánico resueltos
Solución:
Primero aplicamos el trabajo realizado por la fuerza de 45N :
$\displaystyle T=(45N)(10m)=450J$
Ahora despejamos a la fuerza:
$\displaystyle F=\frac{T}{d}=\frac{{450J}}{{5m}}=90N$
Que sería nuestra respuesta.
Solución:
Para este caso, obtenemos el trabajo primeramente:
$\displaystyle T=(80N)(3m)=240J$
Ahora, utilizamos la fórmula de la energía potencial para despejar a la altura.
$\displaystyle {{E}_{p}}=T=mgh$
Es decir:
$\displaystyle h=\frac{T}{{mg}}=\frac{{240J}}{{(15kg)(9.8\frac{m}{{{{s}^{2}}}})}}=1.63m$
La respuesta es, 1.63 metros.
Solución:
Aplicamos solamente la fórmula, teniendo en cuenta que contamos con los datos necesarios para la solución:
$\displaystyle T=Fd=\left( {5000N} \right)\left( {15m} \right)=75000$
Lo que vendría a ser nuestro resultado.
Solución:
Aplicamos la fórmula del trabajo, teniendo en cuenta que la fórmula del trabajo la podemos expresar también con la altura en lugar de la distancia:
$\displaystyle T=Fd=Fh$
Entonces, obtenemos:
$\displaystyle T=Fh=(8kg)(9.8\frac{m}{{{{s}^{2}}}})(4m)=313.6J$
Sería nuestro resultado.
Solución:
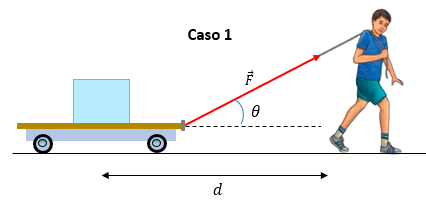
Caso 1: Anotemos los datos que tenemos para el primer caso.
Datos:
F = 20 N
d = 8 m
θ = 60°
Considerando los datos anteriores y sustituyendo en nuestra fórmula, tenemos.
$\displaystyle T=Fd\cos \theta $
$\displaystyle T=\left( 20N \right)\left( 8m \right)\cos 60{}^\circ $
$\displaystyle T=\left( 20N \right)\left( 8m \right)\cos 60{}^\circ =80Nm=80J$
Lo que sería igual a 80 Joules.
Veamos el siguiente caso 😎
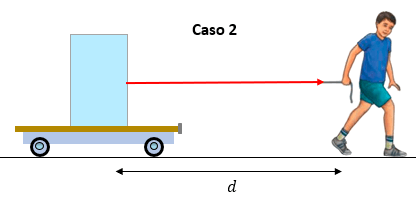
Caso 2: Anotemos los datos que tenemos para el segundo caso.
Datos:
F = 20 N
d = 8 m
θ = 0°
Basándonos en nuestros datos y anotándolos en la fórmula, tendremos:
$\displaystyle T=\left( 20N \right)\left( 8m \right)\cos 0{}^\circ =160Nm=160J$
Eso sería un trabajo de 160 Joules, prácticamente el doble de trabajo que el caso 1.
Solución:
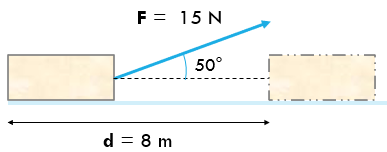
Si analizamos el problema nos vamos a dar cuenta que poseemos una inclinación en dirección al desplazamiento de 8 metros, esto indica que tendremos que usar la fórmula que posee al ángulo tetha. Entonces comenzamos con anotar los datos:
Datos:
F = 15 N
d = 8 m
θ = 50°
Aplicando la siguiente fórmula:
$\displaystyle T=Fd\cos \theta $
Y sustituyendo nuestros datos, obtenemos:
$\displaystyle T=Fd\cos \theta =\left( {15N} \right)\left( {8m} \right)\cos 50{}^\circ =77.13J$
Por lo que el trabajo realizado será de 77.13 J
Solución:
En este problema tenemos dos incisos para resolver, el primero nos pide el trabajo realizado y en el segundo nos cuestiona sobre si se realizó trabajo, comencemos 🙂
a)
Lo primero que haremos será anotar nuestros datos:
Datos:
P = F = 1250 N
d = 2.1 m
Aplicando la fórmula del trabajo y recordando que no tenemos un ángulo, entonces:
$\displaystyle T=Fd$
$\displaystyle T=\left( {1250N} \right)\left( {2.1m} \right)=2625J$
Por lo que el trabajo realizado por la atleta es de 2625 J
veamos ahora el otro inciso
b)
Para este caso debemos ser muy intuitivos de la situación e imaginarlo, ya que el trabajo solo se realiza cuando se aplica una fuerza en la misma dirección de esta, y para este caso la atleta se está desplazando horizontalmente, es decir que no hay componente para poder modificar el trabajo. La única forma en que puede aplicar más trabajo es moviendo o desplazando la pesa más arriba ya que tendríamos una altura mayor. Pero si camina hacia cualquier lado horizontal no habría trabajo. Por lo que concluimos que si se desplaza 3 metros, no habrá ningún trabajo.
Ejercicios para practicar de Trabajo Mecánico
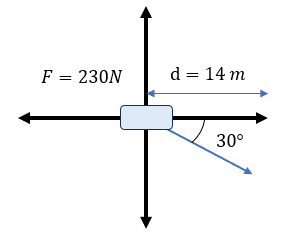
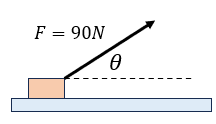
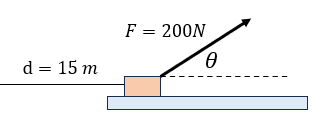
-
Me parece un tema interesante y importante porque
Describe la relación entre la fuerza aplicada y el movimiento de un objeto.
Permite calcular la energía transferida entre sistemas.
Es fundamental para entender muchos fenómenos naturales y tecnológicos.★★★★★
-
Excelenteee!!!!
★★★★★
-
Gracias por ayudar
-
Problema 9: para el ángulo de 30° sería 1870.6 no 1670.6, creo que ahí ha habido un error o no se si sea yo el confundido.
-
Muy bien gracias
25 Deja tu comentario
Deja una respuesta

Estos temas te pueden interesar